[Author’s note: Another old paper makes it online!]
A while back I took a class on ancient chinese philosophy, taught by David Wong (who is great, by the way.) One of the things that Professor Wong noted was the similarity between modern-day ethical debates surrounding effective altruism and the ancient dispute between Mozi and Mengzi. I dug a little deeper and made a list of all the similarities I could think of; this is that list. Comments welcome:
https://docs.google.com/document/d/1xlGJ8_mV2vRB8ig1jIqsdWVPFcoNQXqYxBeBWc08NzE/edit?usp=sharing
I’m sufficiently impressed by these similarities that I think it is fair to say that Mozi and Mengzi really were talking about the same issues that feature prominently in debates about EA today; they were even making many of the same arguments and taking many of the same positions. I think this is really cool. If I ever teach intro to philosophy (or ancient philosophy, or non-western philosophy, or intro to ethics) in university, I intend to include a section on Mozi/Mengzi/EA.
Acausal Trade slideshow
[Author’s note: Still working through a backlog of old stuff to put up. These are the slides from a presentation I made two years ago. If you have any questions about it, feel free to ask me!]
https://docs.google.com/presentation/d/1r4byVsmkTxzO86VRc7CRyxf8AT6_xXRGcb4TDSjspkA/edit?usp=sharing
An analogy for the simulation argument
To people already familiar with the argument, this may be old news. It’s an analogy to help people feel the intuitive force of the argument.
Suppose the following: New diseases appear inside people all the time. Only one in ten diseases is contagious, but the contagious diseases spread to a thousand other people, on average, before dying out. The non-contagious ones don’t spread to anyone else. You get sick. You haven’t yet gone to the doctor or googled your symptoms; given the above facts, part of you wonders whether you should bother… after all, 90% of diseases only ever infect one person. So, how likely is it that someone else has had your disease before?
Draw a Venn diagram with two circles: “First victim” and “contagious.” This makes three interesting categories:
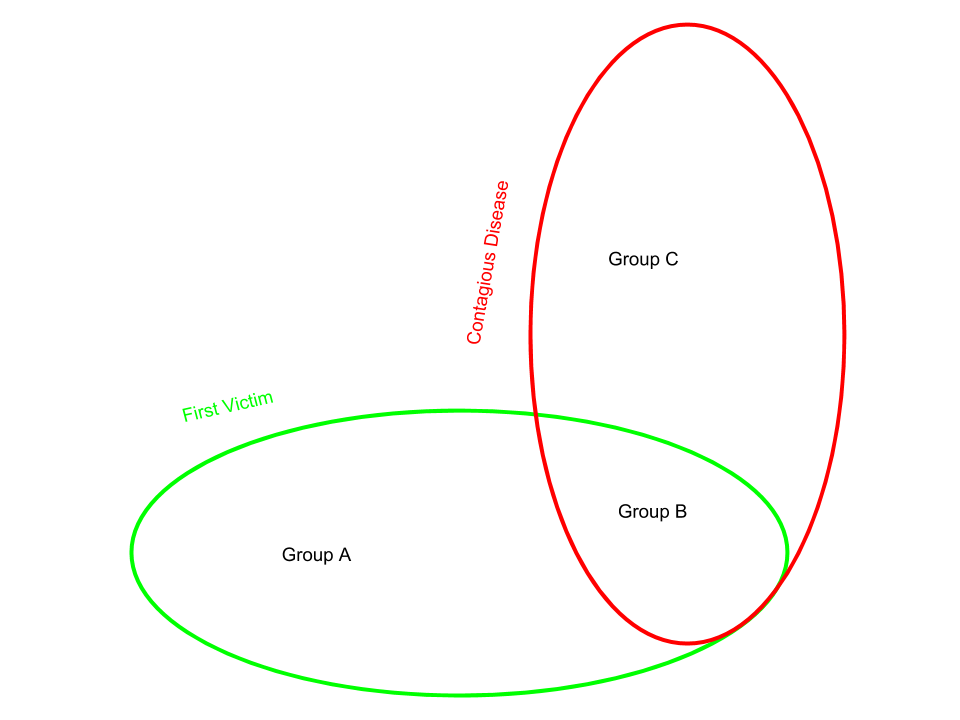
A = First victims of noncontagious diseases
B = First victims of contagious diseases
C = Nonfirst victims of contagious diseases
Since only one in ten diseases is contagious, B/A = 1/9.Since contagious diseases spread to a thousand people on average, B/C is 1/1000. It follows that C/(A+B+C) = 100/101.
Since you know you are diseased, you should assign credence to each hypothesis “I’m in A” “I’m in B” “I’m in C” equal to the fraction of diseased people who are in that category, at least until you get evidence that you would be more likely to get in one category than another.
(For example, if you google your symptoms and get zero hits, that’s evidence that is more likely to happen to people in group A or B, so you should update to be less confident that you are in group C than the base rate would suggest.)
So you are almost certain to be in category C, since they make up 100/101 of the total population of diseased people, and at the moment you don’t have any evidence that is less likely to happen to people in category C than people in the other categories. So it’s almost certain that other people have had your disease already, even though 90% of diseases only ever infect one person.
In the simulation argument, the reasoning is similar.
Suppose that 90% of non-simulated civilizations never create ancestor sims, but that the remaining 10% create 1000 each on average. Then most civilizations are ancestor-simulated.
Do we have any evidence that is more likely to happen to people who are ancestor-simulated than people who are not, or vice versa?
You might think the answer is yes: For example, simulated people are more likely to see things that appear to break the laws of physics, more likely to see pop-up windows saying “you are in a simulation,” etc.
But Bostrom anticipates this when he restricts his argument to ancestor simulations. Ancestor simulations are designed to perfectly mimic real history, so the answer is no: Someone in category C is just as likely to see what we see as someone in category B or A.
So even if we rule out non-ancestor-simulations entirely, the argument goes through: Most civilizations with evidence like ours are ancestor-simulated, and we don’t have any reason to think we are special, so we are probably ancestor-simulated. And of course, we shouldn’t rule out non-ancestor-simulations entirely, so the probability that we are simulated should be even higher than the probability we are ancestor-simulated.
(Clarificatory caveat: Bostrom’s argument is NOT for the conclusion that we are in a simulation; rather, it is a triple-disjunct. In the framing discussed here, Bostrom leaves open the possibility that Group A is extremely large relative to Group B, large enough that it is bigger than B and C combined.)
Great Map of the Mind
We have all these theories and debates about parts of the mind; why not make a big map to show how they all fit together?
Obviously, minds aren’t all the same. But having a map like this helps us organize our thoughts, to better understand our own minds and the minds we are trying to design and reason about. I’d love to see better versions, or elaborations of this one, or entirely different mind-designs.
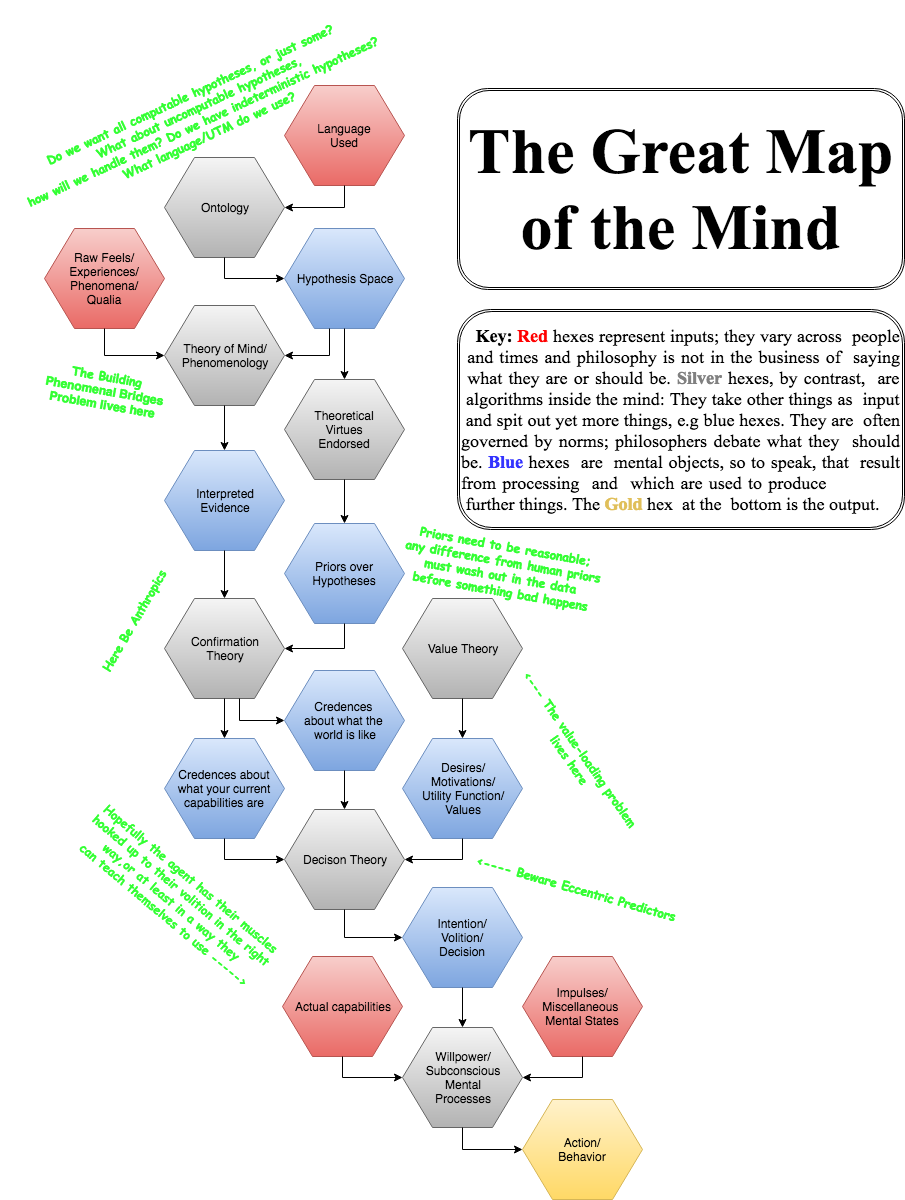
If you want the original document: Get draw.io, then follow this link and click “Open with…” and then select draw.io. I’d love it if people spin off improved versions.
Not Your Grandma’s Phenomenal Idealism
[Author’s note: Now that I’m finally putting my stuff online, I have a backlog to get through. This is a term paper I wrote three years ago. As such, it reflects my views then, not necessarily now, and also it is optimized for being a term paper in a philosophy class rather than an academic paper for an interdisciplinary or AI-safety audience. Sections I and II sketch a theory, Lewisian Phenomenal Idealism, which is relevant to consciousness, embedded agency, and the building-phenomenal-bridges problem. The remaining sections defend it against objections that you may not find plausible anyway, so feel free to ignore them. Here is the gdoc version if you want to give detailed comments or see the footnotes.]
Not Your Grandma’s Phenomenal Idealism
[T]he structure of this physical world consistently moved farther and farther away from the world of sense and lost its former anthropomorphic character …. Thus the physical world has become progressively more and more abstract; purely formal mathematical operations play a growing part. —Max Planck
When you see something that is technically sweet, you go ahead and do it and argue about what to do about it only after you’ve had your technical success. That is the way it was with the atomic bomb. —Robert Oppenheimer
It started as just a weird theory invented to serve as a counterexample, but now I’m halfway convinced that it’s true. —Daniel Kokotajlo
In the second chapter of his forthcoming book, “Idealism and the limits of conceptual representation,” Thomas Hofweber argues that phenomenal idealism is not worth taking seriously, on the grounds that it conflicts with what we know to be true—for example, we know that there were planets and rocks before there were any minds. (p12) I think this is too harsh: While we may have good reasons to reject phenomenal idealism, geology isn’t one of them. I think that phenomenal idealism should be taken as seriously as any other weird philosophical doctrine: The arguments for and against it must all be considered and balanced against one another. I don’t think that empirical considerations, like the deliverances of geology, have any significant bearing on the matter. The goal of this paper is to explain why.
I will begin by locating phenomenal idealism on a spectrum of other views, including reductive physicalism, which I take to be the main alternative. I will then present my own version of phenomenal idealism—“Lewisian Phenomenal Idealism,” or LPI for short—which I argue neatly avoids most of the standard objections to phenomenal idealism. It’s a proof of concept, so to speak, that phenomenal idealism is worth taking seriously. Finally, and most importantly, I’ll defend LPI against the strongest objection to it, the objection that it illegitimately reassigns the referents of the terms in the sentences we know to be true, and hence conflicts with what we know to be true.
I: Lewisian Phenomenal Idealism
Hofweber’s definition of phenomenal idealism is as follows:
The immediate objects of perception are thus phenomena, mental things which we are directly aware of. So far this is just a view about perception. But what turns it into idealism is to add that the objects are or are constructed from these phenomena, somehow. The material world is not a mind-independent world that we see indirectly, via the phenomena, nor is it represented by the phenomena. Instead, the phenomenal world is the material world. The phenomena do not represent the objects, but constitute them. (p20)
Though Hofweber’s definition above commits phenomenal idealism to two theses—one about perception, and another about ontology—I will only focus on the latter, since it generally taken to be more central. The phenomenal idealist position that I aim to defend is a version of the “Reductive Phenomenal Idealism” on the following spectrum:
-
- Eliminative Physicalism: There are physical objects, but no minds or experiences.
-
- Reductive physicalism: There are both, but only physical objects are fundamental: Minds and experiences are constituted by physical objects.
-
- Dualism: There are both fundamental physical objects and fundamental minds and experiences.
-
- Reductive Phenomenal Idealism: There are both, but only minds/experiences are fundamental: Physical objects are constituted by minds and experiences.
- Eliminative Phenomenal Idealism: There are minds and experiences, but no physical objects.
Based on Hofweber’s definition and on that given by Foster (a contemporary defender of phenomenal idealism) it is fair to characterize Phenomenal Idealism for our purposes as just Reductive Phenomenal Idealism above. I located it on this spectrum to highlight the parallel between reductive phenomenal idealism and the reductive physicalism that we all know and love: At least at first glance, they both posit the same entities, and the same number of fundamental ontological kinds; the only difference is the direction of fundamentality.
Lewisian Phenomenal Idealism (LPI) has four components: An ontological claim, a philosophy of science claim, an empirical claim, and a revisionary reductive analysis of our talk about physical objects. It will take a while to explain each of them in sufficient detail:
LPI Ontology: Fundamentally, there are only minds and experiences.
I intend to avoid the issue of how minds and experiences are related—are they two separate kinds? Is one a property or relation of the other? It should be irrelevant for the purpose of this paper.
LPI Philosophy of Science: Laws of Nature are as David Lewis’ Best Systems Theory says: They are the theorems of the deductive system that describes the world with the best balance of simplicity, strength, and fit. (Lewis 1980)
This requires a bit of explanation. The idea is that which minds exist, and which sequences of experiences they have, can be described by a variety of deductive systems. Some are very detailed, accurately describing everything there is to describe, but are very complex; others are rather simple, but miss out on a few details. The best system is the hypothetical system that achieves the best balance of simplicity, strength, and fit. The Laws of Nature, then, are defined in terms of the best system. Lewis says they are the theorems of the best system; I’ll eventually go for something a little more nuanced, but that will do for now.
The Best Systems account of lawhood is controversial, but I’m happy to accept the consequences for now. If the worst that can be said of LPI is that it relies on Lewis’ theory of lawhood, this paper is a success.
LPI Empirical Claim: The Best System is of the following form: For each structure of type M in the theorems of [insert physicalist Best System here] passing through a sequence of states S1,…Sn, there exists a mind which has the sequence of experiences given by f(S1),…f(Sn).
This requires quite a lot of explanation. I’ll start by explaining what a physicalist Best System would look like, given what we know of physics. It would have some description of which objects in which relations exist in the initial condition, and then some description of how the system evolves over time. Both descriptions would be heavily constituted by the deliverances of ideal physics. It is this description, this Best System, that LPI places in the brackets above. Importantly, I described things this way for convenience only. LPI does not parasitically depend on physicalism; I put it that way for ease of exposition and to highlight the similarities between the two theories. Technically LPI would have [insert description of initial conditions and rules for how they evolve over time]; the idea is that whatever evidence physics gives us, according to physicalism, for the rules and conditions of the Best System is, according to LPI, evidence instead for the rules and conditions of the bracketed section of the Best System.
Now, reductive physicalism follows up its account of the Best System with a revisionary reductive analysis of mind/experiences, so that the theory as a whole can posit minds and experiences as well as fundamental physical objects. This reductive analysis is supposed to be partially the result of philosophy (armchair theorizing about what sorts of functional, behavioral, or structural properties a system must have in order to count as a mind) and partially the result of psychology (empirical data on which neurochemical structures lead to which experiences under which conditions). Never mind the details, the point is that according to reductive physicalism there is some type M such that a mind exists whenever there is a physical structure of type M. According to LPI, then, there is some type M such that a mind exists whenever in the bracketed section of the Best System there is a structure of type M. Something similar can be said about the function f. Whereas according to reductive physicalism, philosophy and psychology tell us how minds and experiences supervene on physical structures, according to LPI, philosophy and psychology tell us about sections of the Best System which describes which minds/experiences there are.
One important difference between LPI and reductive physicalism is that for reductive physicalism, all this stuff about minds and experiences is part of a revisionary reductive analysis, separate from the Best System for describing the world; by contrast, for LPI, this is all part of the Best System. More on this point in Section II.
LPI Reductive Analysis: Our talk about physical objects is analyzed as talk about the bracketed section of the Best System. Our talk about the Laws of Nature that the sciences discover is analyzed as talk about the bracketed section as well. Indeed for convenience we can think of the bracketed section as being a “simulation” of the world that the physicalist thinks is actual. Most ordinary conversation is analyzed as talk about the simulation.
I’ll supplement this with two examples: When a physicist says “We just discovered that there are exactly 13 kinds of fundamental particle,” their claim can be analyzed as “We just discovered that the part of the Best System which simulates a bunch of fundamental particles, simulates exactly 13 kinds.” When an atheist geologist says “There were rocks and planets for billions of years before there were minds,” their claim can be analyzed as “The part of the Best System which simulates a bunch of objects evolving over time, simulates rocks and planets billions of simulation-years before it simulates objects of type M.”
II: Discussion
Before moving on to Hofweber’s criticism of phenomenal idealism, it is worth taking the time to discuss a few issues that arise independently.
First, LPI may strike some readers as extremely suspicious. Isn’t it ad hoc? Doesn’t it basically steal all the achievements of reductive physicalism and claim them as its own? It seems like an accommodation, rather than a prediction, of the data.
I have three responses to this worry. The first is that there is nothing wrong with stealing the achievements of a successful theory, if all that means is making a new theory that combines the same predictive accuracy with additional desirable traits. Indeed in most cases when this happens, all the reasons we had for believing the old theory transfer over into reasons to believe the new theory. This is, in general, how human knowledge progresses.
My second point is a warning not to overstate the successes of reductive physicalism. Physics has been successful; geology has been successful; psychology and neuroscience have been successful, etc. But they would have been equally successful if LPI and not reductive physicalism had been the dominant ideology for the past two centuries.
My final point is that the empirical claim LPI makes actually flows fairly naturally from the Ontological and Philosophy of Science claims it makes. Our minds are extremely complex. If the Best System describing minds/experiences did so directly, by specifying which experiences were had, in which order, it would have to be similarly complex. Arguably this Best System would be more complex than the one posited by LPI’s Empirical Claim! By describing minds/experiences indirectly, by simulating a large physical universe that evolves according to simple laws, and then extracting descriptions of minds and experiences from that simulation, the Best System can compress the data significantly. Hence, arguably, LPI Empirical Claim is actually predicted by the conjunction of Occam’s Razor, the datum that complex minds exist, and the ontological and philosophy of science claims made by LPI. This puts LPI on the same footing as physicalism with respect to predicting the world as we find it.
All that being said, LPI is admittedly more complex than reductive physicalism. However complicated the Best System is according to reductive physicalism, the Best System according to LPI will be that and then some. (The additional complexity will be approximately the sum of the complexity of Type M and the complexity of the function f.) So, other things equal, by Occam’s Razor we ought to prefer reductive physicalism to LPI.
Other things are not equal. There are arguments against reductive physicalism, which, if successful, rule it out before Occam’s Razor can be brought to bear. These are the arguments that have occupied the literature on consciousness for decades and possibly centuries: the “explanatory gap,” the zombie thought experiment, the Mary’s Room case, etc. I am not trying to say that these arguments are correct; my point is just that LPI can’t be ruled out straightaway by Occam’s Razor. The arguments must be considered first.
Finally, I suspect that LPI may solve many of the problems in philosophy of mind. It seems to provide a non-arbitrary connection between the mental and the physical, and explains how that connection holds. It accounts for our intuitions about qualia, the unity of consciousness, etc. It resolves worries about vagueness and borderline cases of consciousness/personhood. It even suggests a principled answer to questions about the persistence of personal identity over time! It does this in the same way that dualism does it—by positing fundamental minds/experiences subject to contingent laws. Questions about minds and experiences become normal empirical questions, no more mysterious than questions about the gravitational constant or the composition of water. Unlike dualism, though, LPI doesn’t run into problems trying to connect mind and matter—there is no overdetermination, no causal inaccessibility, etc.
I should qualify the above by saying that I haven’t worked out the implications of LPI in any detail yet; I may be wrong about its advantages. My point in mentioning these speculative ideas is to garner support for the thesis of this paper, which is that LPI—and by extension, phenomenal idealism more generally—shouldn’t be ruled out straightaway as conflicting with what we know to be true. On the contrary, it’s an interesting philosophical theory that deserves proper philosophical consideration. In the next three sections, I’ll lay out and discuss Hofweber’s arguments against this thesis.
III: The Coherence Constraint
In this section I will lay out Hofweber’s argument against phenomenal idealism in detail. According to my categorization, he has four arguments for why phenomenal idealism conflicts with what we know to be true. They aren’t meant to all apply at the same time; different arguments apply to different versions of phenomenal idealism. In this section I will show that LPI avoids the first three arguments. The remaining argument, which I take to be the most important, will occupy the rest of the paper.
Hofweber’s arguments revolve around the Coherence Constraint:
Coherence Constraint: An acceptable form of idealism must be coherent with what we generally take ourselves to know to be true. (p12)
Presumably the Coherence Constraint is to be generalized to all metaphysical theories, not just idealism. A helpful gloss on it follows:
To accept the coherence constraint is closely tied to thinking of metaphysics as being modest with respect to other authoritative domains of inquiry. Although any scientific result might be mistaken after all, metaphysics should not require for its work that this turns out to be so. It should do something over and above what other authoritative parts of inquiry do. It asks questions whose answer is not given by and not immediately implied by the results of the mature sciences. Applying this to idealism it means that idealism must be compatible with us living on a small planet in a galaxy among many. It must be compatible with our having a material body in a material world, and so on. It can make proposal about what matter is, metaphysically, or other things, but whatever it is supposed to be, it must be compatible with and coherent with the rest. This is the coherence constraint, and any form of idealism worth taking seriously must meet it. (p12)
I’ll have a lot to say about this in the next two sections. For now, I’ll briefly discuss how LPI avoids the first three arguments:
Argument One: Problem of Intersubjectivity
The idea behind this problem is that one of the things we know to be true is that there are other minds like us, and that their experiences are coordinated with ours—when I type the word “Porcupine” on my screen, I know that eventually someone (In this case Hofweber himself) will see the word “Porcupine” on his. On theistic versions of phenomenal idealism, this can easily be explained: God coordinates everyone’s experiences so that they match up in this way. But LPI is not theistic; can it explain how all our experiences are coordinated?
Yes it can. The Laws which govern minds and experiences involve a “simulation” of physical objects, and which minds there are and which experiences they have are determined by this simulation. If minds had uncoordinated experiences, the laws governing them would not be of the form specified by LPI Empirical Claim, and indeed would probably be much more complicated.
There is a legitimate worry about how LPI can explain the coordination of our experiences by reference to these Laws, since the Best System in which they are based is merely a description of which minds there are and which experiences they have. However this worry is a general problem with Lewisian accounts of lawhood, and not a problem with LPI in particular.
Argument Two: Problem of Unobserved Objects
The idea behind this problem is that one of the things we know to be true is that there were rocks and planets before there were minds—geology and astronomy have discovered this, at least if we assume atheism is true and there are no parallel universes with aliens in them etc. More generally, it seems like one of the things we know to be true is that there are objects which have not, are not, and never will be observed by any mind. How does LPI account for this fact?
It does so with its revisionary reductive analysis of objects. Talk about physical objects is analyzed as talk about structures in the simulation. When an atheist geologist says “There were rocks and planets for billions of years before there were minds,” their claim is analyzed as “The part of the Best System which simulates a bunch of objects evolving over time, simulates rocks and planets billions of simulation-years before it simulates objects of type M.” When an atheist physicist says “There are objects which have not, are not, and never will be observed by any mind” their claim is analyzed as “In the simulation, there are objects which never get observed by any mind.”
In general, LPI marks as true all the same sentences that ordinary physicalism marks as true—sentences like “There were rocks before there were minds,” “Some objects never get observed,” “There is a computer in front of me right now,” etc. Of course, LPI achieves this only by changing the referents of the relevant sentences: instead of referring to external, mind-independent objects, they refer to structures in a simulation, which is itself a component of the Best System for describing which minds/experiences there are. This is exactly what one should expect; of course a reductive phenomenal idealist theory is going to say that our talk about physical objects does not refer to external, mind-independent things, since reductive phenomenal idealism by definition says that physical objects are reduced to mind-dependent things. Other reductive phenomenal idealist theories reduced physical objects to counterfactual experiences, or possible experiences; LPI does something different, but similar in kind.
Nevertheless you might think that this changing-of-the-referents, this reductive analysis, is illegitimate. This is precisely the move made by Argument Four, and responding to it will occupy Sections IV and V of this paper.
Argument Three: Not Really Phenomenal Idealism
At various points in his book, Hofweber considers versions of phenomenal idealism that perhaps escape his criticisms—except that they do so at the cost of their phenomenal idealist credentials. One example is a version of pantheism, which says that physical objects are aspects of god—in particular, ideas in God’s mind. (p24) In this case, Hofweber says, physical objects inhabit a world that is independent of our minds at least, even though it might not be independent of all minds. It isn’t physicalism, but it isn’t phenomenal idealism either. Perhaps LPI has done the same; perhaps it avoids Hofweber’s arguments against phenomenal idealism because it is not really phenomenal idealism.
This argument is one of the reasons that I decided to build LPI around a Lewisian conception of lawhood. I can see how, arguably, if laws were self-sufficient entities in some sense, one might say that the “simulation” is really a mind-independent external reality. But since according to LPI physical objects are just structures in the simulation, and the simulation is just a part of the Best System, and the Best System is just a description of which minds there are and which experiences they have, physical objects really are mind-dependent according to LPI. And they are dependent on minds like ours, since minds like ours are the only minds there are.
IV: The No Reinterpretations Objection
The No Reinterpretations Objection revives the Problem of Unobserved Objects by rejecting LPI’s revisionary reductive analysis of our talk about physical objects:
The idealist must meet the coherence constraint by making clear that what their view is is coherent with what we know to be true. It is not enough to do this to assign some meaning to the words ‘there were dinosaurs’ and show that with this meaning it is compatible with idealism that ‘there were dinosaurs’ is true. Instead, the idealist must show that the statement is compatible with idealism with the meaning it in fact has, i.e. they must show that there were dinosaurs (before there were humans) is compatible with idealism. As such the idealists proposal about the meaning of `there were dinosaurs’ must be taken as an empirical proposal about the actual meaning of this sentence in English. It is one thing to show that idealism is compatible with the truth of this sentence given some assignment of meaning to this sentence, and quite another to show it is compatible with the truth of the sentence with the actual meaning of it. (p26)
As I understand it, Hofweber is objecting to the “Revisionary” part of LPI’s revisionary reductive analysis. He thinks that statements about physical objects only cohere with LPI if they do so given the meanings that they in fact have, in English. It doesn’t count if they cohere with LPI given different meanings supplied by LPI. On the face of it, this objection is very plausible. Any set of sentences can be made coherent with any other set of sentences, if you are allowed to change the meanings of the sentences! It seems that LPI is helping itself to a technique—revisionary reductive analysis—that will allow it to get away with anything.
In this section, I will respond to this basic version of the No Reinterpretations objection. I’ll argue that, in fact, the burden of proof is on Hofweber to go beyond what has been said so far and present a positive argument for the illegitimacy of LPI’s revisionary analysis. In the next section, I’ll examine a later argument Hofweber makes that I construe as an attempt to meet that burden.
I’ll begin by pointing out a tension between endorsing the Coherence Constraint and critiquing LPI in this way. In his elaboration quoted above, Hofweber explicitly permits idealism to “say what matter is, metaphysically.” (p12) Thus Hofweber agrees there is some legitimate middle ground between the bad kinds of revisionary analysis and mere proposals about the English meanings of words. My point so far is that it is unclear where the boundary is; in the remainder of this section, I’ll argue that LPI occupies that acceptable middle ground.
Consideration One:
My first point is that revisionary reductive analysis is a legitimate philosophical and scientific move that has been made successfully many times in the past, and is often attempted today. I’ll give three examples, but many more could be generated if necessary:
-
- Laws Example: Laws of Nature were once taken more literally, as decrees of God, or at least descriptions of His governance of creation. At some point the scientific community switched to a new concept that didn’t necessitate a Lawgiver.
-
- Relativity Example: Space and time are intuitively thought of as distinct; even among most normal English speakers today, it is fair to say that space means Euclidian space and time means something else. Yet according to relativity, there is no such space and no such time in the actual world.
- Physicalism Example: Minds were for the longest time thought to be essentially immaterial and unified. This was no “folk” belief either—the best scientists and philosophers of the modern era thought this. Reductive physicalism eventually came along and overturned this view, saying that minds are neither immaterial nor unified.
I think that the Physicalism example is particularly close to what LPI is trying to do: Recalling the physicalism-dualism-idealism spectrum, LPI is advocating that we revise our understanding of the world in the same way that Physicalism did, only in the opposite direction.
I hold these up as examples of revisionary analysis, but this can be disputed. For example, one might say instead that the meaning of “minds” stayed the same, because it was never committed to immateriality and unity in the first place. Rather, “minds” meant something like “That in virtue of which things can think, feel, and choose” or perhaps “The relevant cause of my ‘mind’ mental representation tokens.”
I’m happy to accept this possibility, because if we can convince ourselves that the meaning of our words was preserved in the examples given, i.e. if we can convince ourselves that they aren’t really examples of revisionary analyses, then we should also be able to convince ourselves that LPI isn’t really performing a revisionary analysis either. Whatever it is that Physicalism did when it convinced people that minds weren’t really immaterial unities—I claim that LPI is trying to do the same thing, but in the opposite direction.
It’s worth mentioning a point made by Foster and Smithson: Often when people adopt a radical change in their ontological beliefs, they initially express the change by saying “I now believe that there is no X!” yet then soon after start saying “I still believe there is X, but it isn’t what I used to think it was.” (Foster 1994, Smithson 2015) I remember some of my teachers saying things like this in middle school, when we learned about how material objects are “mostly empty space,” and about how they “never actually touch each other,” etc. Presumably the same thing happened with the examples given above, and presumably the same thing would happen again if we started believing in LPI. I take this as evidence that the sort of thing LPI is doing is closer to “say[ing] what matter is, metaphysically” than to “conflicting with what we know to be true.” (Hofweber p12) It is evidence that our cherished knowledge of physical objects is not knowledge that there are physical-objects-as-physicalists-define-them, but rather knowledge that there are physical objects-according-to-some-broader-definition.
Consideration Two: The rough idea here is that we want our epistemology to be reasonably open to change, so that we can converge on the truth from a wide variety of starting points. We don’t want which beliefs are permissible to depend on non-truth-tracking historical accidents. To illustrate:
LPI Takeover Case: Suppose that I convert some wealthy donors to belief in LPI, and we engage in a decades-long covert proselytization process in which we change the way young scientists are taught to think about physical objects. We get the textbooks changed to use definitions of “object” that are neutral between the LPI definition and the physicalist definition, etc. In other words, we change the meaning of the term “object” in English, so that it is more permissive. Once we have accomplished this, we introduce LPI into the philosophical discourse, confident that it now passes the Coherence Constraint.
Clearly something has gone wrong here. Yet this is, I claim, relevantly similar to what happened with reductive physicalism. Not that there was a conspiracy or anything; just that the meanings of our terms shifted over time, in a way that allowed for the possibility of reductive physicalism, but not in a way that particularly tracked the truth—it’s not like the meanings of our terms shifted because we found empirical evidence that reductive physicalism (as opposed to dualism) was true. Perhaps the shift was motivated by philosophical considerations; people became dissatisfied with dualism as an explanation for mental causation, etc. But in that case, the conclusion should be that the shift in meaning in the LPI Takeover Case is legitimate if there are good philosophical reasons motivating it. And if that’s the case, then we can’t yet rule out LPI as conflicting with what we know to be true, because we have to consider the philosophical arguments for and against it first. And that’s precisely the thesis of this paper.
Consideration Three: Contemporary analytic philosophy is full of attempted revisionary analyses. Philosophers debate definitions of objective chance, universals, mathematical objects, composite objects, vague objects, etc. and they debate whether or not these things exist, and if so, under what definition. Sometimes attention is paid to the actual English meanings of our terms, but often it is not. One hears things like “There are no chairs, only particles arranged chair-wise,” and “There aren’t really any numbers; they are just convenient fictions.” These are examples of the english meanings being kept but the associated knowledge claims rejected. The examples I gave earlier are examples of the opposite strategy. Thus, LPI is very much situated within a broader tradition; what it is doing is normal and accepted.
Maintaining his consistency, Hofweber goes on to explicitly reject some of the attempts I mention above—specifically, nominalism in mathematics and eliminativism about ordinary objects. (Chapter 7) His rejection of LPI’s revisionary analysis is part of a broader rejection of a whole class of similar analyses in contemporary analytic philosophy.
In the next section I will evaluate his argument for this; for now I stick to the more moderate conclusion—which I take to have established by now—that the burden of proof is on Hofweber: In the absence of a good positive argument against the legitimacy of LPI’s revisionary analysis, we ought to accord it the same legitimacy as all the other historically successful and currently accepted attempts at revisionary analysis. This doesn’t mean we should accept LPI, of course—it just means that LPI should be accepted or rejected on the basis of all the arguments for and against it, and not simply rejected as conflicting with what we know to be true.
V: The Argument Against Reinterpretation
Elsewhere in his book (Chapter 7), Hofweber presents an argument for the existence of ordinary composite objects and against certain views in mereology, which probably count as “Eliminative Physicalism” under my classification. I believe this argument can be generalized to apply to the case of LPI as well. In this section I’ll first lay out the argument as I construe it, and then attempt to poke three holes in it.
Hofweber’s Argument:
-
- (P1) Skepticism is false. (p251)
- (P2) If skepticism is false, then we are defeasibly entitled to the beliefs we form on the basis of perception. (p251)
- (L3) (From P1 & P2) We are defeasibly entitled to the beliefs we form on the basis of perception. (p251)
- (P4) Some of the beliefs we form on the basis of perception are incompatible with LPI. (p252)
- (L5) (From L3 and P4) So there are some beliefs which we are defeasibly entitled to, which are incompatible with LPI. (p252)
- (P6) If our entitlement to beliefs is defeated, it is either rebutted or undercut, and if it is undercut, either our entitlement to all perceptual beliefs is undercut or not. (p252)
- (P7) If our entitlement to all perceptual beliefs is undercut, then skepticism is true. (p253)
- (L8) (From P1 & P7) So it’s not the case that our entitlement to all perceptual beliefs is undercut. (p253)
- (P9) (With support from L8) Our entitlement to the beliefs mentioned in L5 (the ones that are incompatible with LPI) is not undercut. (p254)
- (P10) If our entitlement to those beliefs is not undercut, we have overwhelming empirical evidence for them. (p258)
- (L11) (From L5, P9, & P10) So there are beliefs formed on the basis of perception which are incompatible with LPI, which are not undercut, and which we have overwhelming empirical evidence for. (p257-261)
- (P12) Beliefs for which we have overwhelming empirical evidence cannot be rebutted. (p261-263)
- (C13) (From L3, L11 & P12) So there are beliefs incompatible with LPI, for which we have overwhelming empirical evidence, and we are entitled to those beliefs. (p263)
Since the original argument is about composite objects rather than mind-independent objects, I’ve had to modify a few of the premises. In particular, the relevant beliefs posited by P4 as incompatible with LPI are things like “There were rocks before there were humans,” and “I see a rock over there right now.” Crucially, terms like “rock” in these beliefs are supposed to be definitively incompatible with LPI. It’s not merely that terms like “rock” don’t mean “rock-structure in the LPI simulation;” they have to also not mean “whatever usually causes rock-appearances” or “the most natural existing referent for my use of the term ‘rock,’” or “something, I know not what, which I am justified in believing exists when I am appeared to rockly.” None of these meanings, even though they are neutral between physicalism and idealism, will do. P4 is saying that we form beliefs on the basis of perception which are not neutral between LPI and physicalism; rather, they are definitively incompatible with LPI.
I will accept P4, with qualifications: Given the above, these beliefs are probably not universally shared; many people probably form beliefs on the basis of perception that are weak enough to be compatible with LPI. Moreover, as Hofweber admits, (p254) these beliefs are contingent: If our culture, education system, and/or brain chemistry were different, we would instead form other, very similar beliefs that would allow us to function in all the same ways without being incompatible with LPI. Finally, LPI is far from alone as a theory which many people form perceptual beliefs against: Reductive physicalism and atheism, for example, are both theories which are incompatible with the perceptual beliefs of many (and perhaps even most) people.
The two premises I find problematic are the ones that Hofweber spends the most time justifying: P9 and P10. In the remainder of this section, I’ll lay out each of his arguments and explain why I don’t think they work.
Premise 9: (With support from L8) Our entitlement to the beliefs mentioned in L5 (the ones that are incompatible with LPI) is not undercut.
Hofweber says (and I agree) that the issue of undercutting in this case comes down to whether or not we have reason to think that the aforementioned beliefs track the truth. Hofweber considers an argument that (in the case of object composition, which his argument is geared towards) they don’t: In the possible world in which there are only simples arranged cup-wise, but no cup, we would still form the same perceptual beliefs in cups. So our belief in cups doesn’t track the truth of whether or not there are cups. (p254) Hofweber responds thus:
The counterfactual situation relevant to evaluate the counterfactual conditional about my cup not being there isn’t one where the simples are still there, but they somehow don’t compose a cup, but rather one where both the simples and the cup are gone. But then nothing would cause me to believe in a cup in front of me, and so my cup beliefs track the cup facts: all things being equal, I wouldn’t have that belief if there wasn’t a cup. (p255)
Converting this argument to work against LPI, Hofweber would presumably say that the beliefs we form on the basis of perception (and which are incompatible with LPI) track the truth, and that they do so because the relevant counterfactual in which they are false is the one in which e.g. we aren’t looking at anything that looks like a rock, geology finds human bones older than any rock, etc. In that counterfactual, we would not form those beliefs.
I am troubled by this reasoning. It seems to me that both counterfactuals are relevant; a belief can track the truth of some propositions but not others. It seems natural to say that our belief that there is a rock (in the LPI-incompatible sense) directly ahead is counterfactually able to distinguish between worlds in which there is a rock and worlds in which there is open space, but not between worlds in which there is a rock (in the LPI-incompatible sense) and worlds in which there is a rock (in the LPI-analysis sense). So, the thought goes, our belief is partially undercut—the part that has to do with the metaphysical nature of the rock is undercut, but the part that has to do with pretty much everything else, like what will happen if we kick the rock, how we can best avoid the rock, etc. is not. This would rescue LPI.
I expect Hofweber’s response to be that that way lies skepticism; we can extend that line of reasoning to the conclusion that all of our perceptual beliefs are systematically undercut, since there are worlds in which e.g. an evil demon is making us hallucinate everything. (p255)
I have two responses to this. The first is that we might be able to use “prior plausibility” to distinguish between the radical skeptical hypotheses and the non-radical, benignly skeptical hypotheses like LPI, mereological nihilism, and reductive physicalism. Presumably these latter hypotheses have more prior plausibility than the evil demon hypothesis. At any rate, in order to settle just how plausible these hypotheses are exactly, we have to consider the arguments for and against them. So if Hofweber’s argument that LPI shouldn’t be taken seriously depends on an assignment of low prior probability to LPI, then he is begging the question; he must instead first address the philosophical arguments for and against LPI, which is exactly the thesis of this paper.
My second response is that some of the examples I gave in Section IV seem to be similar enough to LPI that Hofweber’s argument here would work against them as well! I think any of them would do, but I’ll go with my favorite: Reductive physicalism. Most of the smartest philosophers and scientists in the 17th century formed beliefs on the basis of perception that were incompatible with reductive physicalism; for example, they thought that minds were immaterial and unified. They could use Hofweber’s argument to say that their beliefs track the truth: The relevant counterfactual in which their beliefs are false is one in which minds don’t even exist, not one in which minds exist but are somehow composed of material objects.
Similarly, one can imagine early scientists who thought of Laws of Nature as being given by a divine Lawgiver saying: “The relevant counterfactual in which there is no Lawgiver is a world in which everything moves about higgledy-piggledy; hence my belief in a Lawgiver on the basis of the regularity in the universe tracks the truth.” Indeed I have actually met people who argued this.
Given what I said in Section IV about how our beliefs oughtn’t depend on historical accidents (Consideration Two) I take these examples to be reductios of Hofweber’s argument.
Premise 10: If our entitlement to those beliefs is not undercut, we have overwhelming empirical evidence for them.
Hofweber takes himself to have established by this point that we have non-undercut entitlement to our beliefs about ordinary objects, but not to beliefs about mere simples arranged object-wise (since we don’t in fact have perceptual beliefs in such things). (p256) Converting this into talk about LPI, we may suppose that Hofweber has established by this point that we have non-undercut entitlement to our beliefs about mind-independent rocks, but not to our beliefs about more-broadly-defined-rocks, because we don’t in fact form the latter beliefs on the basis of perception.
Continuing to describe the converted argument rather than the actual one: Hofweber goes on to argue that this disanalogy compounds constantly into a tremendous empirical success for physicalism and predictive failure for LPI. LPI predicts that there are no mind-independent rocks in front of us; yet perception gives us non-undercut entitlement to believe that there are, every day. Even though LPI might in some sense predict our phenomenal experience just as well as the alternatives, it doesn’t predict certain crucial facts like the above.
As a result, Hofweber claims, science heavily disconfirms LPI: Our current scientific theories are defined using terminology that is inconsistent with LPI, and they are far more predictively accurate than their counterparts that would be defined using LPI’s revisionary analyses. (p261)
Hofweber goes on to say that, given the immense body of scientific and perceptual evidence against LPI, no amount of metaphysical argumentation should convince us that LPI is true. (p263) We can rule it out as conflicting with what we know to be true.
I find this argument problematic as well. It starts with a fairly innocuous premise about an asymmetry in our beliefs about two opposing theories, and ends up with a very strong and surprising conclusion. It smells suspiciously like the “Easy Knowledge/Bootstrapping” case described by Vogel and Cohen. Of course that isn’t a legitimate objection, so here are two:
My first objection is that Hofweber seems to be assuming a very strong form of scientific realism here. Even if we set aside the anti-realists (though they constitute 11.6% of the professional population) the positions that remain, realism and structural realism, generally don’t say that we have overwhelming evidence for the literal truth of our current best theories. Rather, they say that we should accept them for now, while assigning high credence to the possibility that the truth is more nuanced and even that the central terms in our current best theories fail to refer. This caution is motivated by the history of science, which is a history of theory after well-confirmed theory turning out to be false when strictly and literally interpreted, even to the point where their central terms fail to refer. Granted, my worry here only applies to the scientific component of Hofweber’s argument, but I think it generalizes to the basic perceptual component as well. The history of strictly-literally-interpreted theories about ordinary observable objects mirrors the history of strictly-literally-interpreted scientific theories about unobservables.
My second objection is that the mere accumulation of truth-tracking, non-undercut perceptual beliefs does not by itself confer overwhelming evidence. Consider a doctor who examines a patient and comes to the perceptual belief, based on her years of experience, that the patient has a certain rare cancer. Suppose that the doctor knows her perceptions track the truth in cases like these: She gets the right answer 99% of the time. Does she have overwhelming evidence that the patient has the rare cancer? Does continuing to examine the patient again and again give her any more evidence?
The answer to both questions is no, if the cancer is sufficiently rare and if her repeated examinations are not independent. Suppose, as often happens, that the cancer strikes only one in every ten thousand patients, and that her repeated examinations are going to yield the same result, since they are based on the same perceived symptoms and intuitive judgments. Then no matter how many times the doctor examines the patient, her credence that the patient has the rare cancer should not rise above 0.01.
The moral of this story is that prior probabilities/base rates are crucial. Depending on how we like to put it, we can say either that priors are crucial for determining whether or not a reliable belief is undercut, or we can say that they are crucial for determining whether a non-undercut reliable belief constitutes overwhelming evidence. Either way, the lesson is that Hofweber needs to say something about LPI’s prior probability in order for his argument to work. But this will involve examining and engaging with the philosophical arguments for and against LPI, exactly as this paper urges.
VI: Conclusion
I admit that the arguments I have given do not conclusively defend LPI; phenomenal idealism may in fact turn out to violate the Coherence Constraint. This admission comes not from any particular weakness I have identified in my reasoning, but rather from a general worry that I don’t understand Hofweber’s: I’m not used to thinking in terms of entitlement, defeaters, and undercutting; my experience has more to do with credences, priors, and Bayesian updating.
Nevertheless, I think that the arguments presented here are more than strong enough to establish my modest conclusion: that LPI ought not be ruled out as conflicting with what we known to be true. On the contrary, it should be taken as seriously as any other weird philosophical theory, and the arguments for and against it should be explored. We should believe this until proven otherwise; the burden of proof is on Hofweber to do so, and he has not yet met it.
REFERENCES:
Foster, J. (1994) ‘In Defense of Phenomenalistic Idealism.’ Philosophy and Phenomenological Research, Vol. 54, No. 3. September. pp. 509-529
Goldman, A and Beddor, B. (2015) “Reliabilist Epistemology”, The Stanford Encyclopedia of Philosophy (Winter 2015 Edition), Edward N. Zalta (ed.), forthcoming URL = <http://plato.stanford.edu/archives/win2015/entries/reliabilism/>.
Hofweber, T. (2015) Idealism and the Limits of Conceptual Representation. Unpublished draft. The relevant chapters are 1, 2, and 7.
Hofweber, T. (2009) ‘Ambitious, Yet Modest, Metaphysics.’ In Chalmers, Manley & Wasserman (eds.), Metametaphysics: New Essays on the Foundations of Ontology. Oxford University Press 260—289
Ladyman, J. (1998) What is Structural Realism? (Studies in the History and Philosophy of Science vol 29 No 3, pp 409-424.
Lewis, D. (1994) Humean Supervenience Debugged. Mind, Vol. 103.412.
Lewis, D. (1980) A Subjectivist’s Guide to Objective Chance, in R. Jeffrey, ed., Studies in Inductive Logic and Probability, vol II. Berkeley: University of California.
Planck, M. (1996) ‘The Universe in the Light of Modern Physics’, in W. Schirmacher (ed.), German Essays on Science in the 20th Century (New York: Continuum), pp. 38–57.
Roberts, J. (2014) ‘Humean Laws and the Power to Explain.’ For UNC-Hebrew University workshop. Available online at http://philosophy.unc.edu/files/2013/10/Roberts-DoHumeanLawsExplain-talkversion.pdf
Stanford, K. (2001) ‘Refusing the Devil’s Bargain: What Kind of Underdetermination Should We Take Seriously?’ Philosophy of Science, Vol. 68, No. 3, Supplement: Proceedings of the 2000 Biennial Meeting of the Philosophy of Science Association. Part I: Contributed Papers (Sep., 2001), pp. S1-S12
Smithson, R. (2015) ‘Edenic Idealism.’ Unpublished draft.
Moral realism and AI alignment
“Abstract”: Some have claimed that moral realism – roughly, the claim that moral claims can be true or false – would, if true, have implications for AI alignment research, such that moral realists might approach AI alignment differently than moral anti-realists. In this post, I briefly discuss different versions of moral realism based on what they imply about AI. I then go on to argue that pursuing moral-realism-inspired AI alignment would bypass philosophical and help resolve non-philosophical disagreements related to moral realism. Hence, even from a non-realist perspective, it is desirable that moral realists (and others who understand the relevant realist perspectives well enough) pursue moral-realism-inspired AI alignment research.
Different forms of moral realism and their implications for AI alignment
Roughly, moral realism is the view that “moral claims do purport to report facts and are true if they get the facts right.” So for instance, most moral realists would hold the statement “one shouldn’t torture babies” to be true. Importantly, this moral claim is different from a claim about baby torturing being instrumentally bad given some other goal (a.k.a. a “hypothetical imperative”) such as “if one doesn’t want to land in jail, one shouldn’t torture babies.” It is uncontroversial that such claims can be true or false. Moral claims, as I understand them in this post, are also different from descriptive claims about some people’s moral views, such as “most Croatians are against babies being tortured” or “I am against babies being tortured and will act accordingly”. More generally, the versions of moral realism discussed here claim that moral truth is in some sense mind-independent. It’s not so obvious what it means for a moral claim to be true or false, so there are many different versions of moral realism. I won’t go into more detail here, though we will revisit differences between different versions of moral realism later. For a general introduction on moral realism and meta-ethics, see, e.g., the SEP article on moral realism.
I should note right here that I myself find at least “strong versions” of moral realism implausible. But in this post, I don’t want to argue about meta-ethics. Instead, I would like to discuss an implication of some versions of moral realism. I will later say more about why I am interested in the implications of a view I believe to be misguided, but for now suffice it to say that “moral realism” is a majority view among professional philosophers (though I don’t know how popular the versions of moral realism studied in this post are), which makes it interesting to explore the view’s possible implications.
The implication that I am interested in here is that moral realism helps with AI alignment in some way. One very strong version of the idea is that the orthogonality thesis is false: if there is a moral truth, agents (e.g., AIs) that are able to reason successfully about a lot of non-moral things will automatically be able to reason correctly about morality as well and will then do what they infer to be morally correct. On p. 176 of “The Most Good You Can Do”, Peter Singer defends such a view: “If there is any validity in the argument presented in chapter 8, that beings with highly developed capacities for reasoning are better able to take an impartial ethical stance, then there is some reason to believe that, even without any special effort on our part, superintelligent beings, whether biological or mechanical, will do the most good they possibly can.” In the articles “My Childhood Death Spiral”, “A Prodigy of Refutation” and “The Sheer Folly of Callow Youth” (among others), Eliezer Yudkowsky says that he used to hold such a view.
Of course, current AI techniques do not seem to automatically include moral reasoning. For instance, if you develop an automated theorem prover to reason about mathematics, it will not be able to derive “moral theorems”. Similarly, if you use the Sarsa algorithm to train some agent with some given reward function, that agent will adapt its behavior in a way that increases its cumulative reward regardless of whether doing so conflicts with some ethical imperative. The moral realist would thus have to argue that in order to get to AGI or superintelligence or some other milestone, we will necessarily have to develop new and very different reasoning algorithms and that these algorithms will necessarily incorporate ethical reasoning. Peter Singer doesn’t state this explicitly. However, he makes a similar argument about human evolution on p. 86f. in ch. 8:
The possibility that our capacity to reason can play a critical role in a decision to live ethically offers a solution to the perplexing problem that effective altruism would otherwise pose for evolutionary theory. There is no difficulty in explaining why evolution would select for a capacity to reason: that capacity enables us to solve a variety of problems, for example, to find food or suitable partners for reproduction or other forms of cooperative activity, to avoid predators, and to outwit our enemies. If our capacity to reason also enables us to see that the good of others is, from a more universal perspective, as important as our own good, then we have an explanation for why effective altruists act in accordance with such principles. Like our ability to do higher mathematics, this use of reason to recognize fundamental moral truths would be a by-product of another trait or ability that was selected for because it enhanced our reproductive fitness—something that in evolutionary theory is known as a spandrel.
A slightly weaker variant of this strong convergence moral realism is the following: Not all superintelligent beings would be able to identify or follow moral truths. However, if we add some feature that is not directly normative, then superintelligent beings would automatically identify the moral truth. For example, David Pearce appears to claim that “the pain-pleasure axis discloses the world’s inbuilt metric of (dis)value” and that therefore any superintelligent being that can feel pain and pleasure will automatically become a utilitarian. At the same time, that moral realist could believe that a non-conscious AI would not necessarily become a utilitarian. So, this slightly weaker variant of strong convergence moral realism would be consistent with the orthogonality thesis.
I find all of these strong convergence moral realisms very implausible. Especially given how current techniques in AI work – how value-neutral they are – the claim that algorithms for AGI will all automatically incorporate the same moral sense seems extraordinary and I have seen little evidence for it1 (though I should note that I have read only bits and pieces of the moral realism literature).2
It even seems easy to come up with semi-rigorous arguments against strong convergence moral realism. Roughly, it seems that we can use a moral AI to build an immoral AI. Here is a simple example of such an argument. Imagine we had an AI system that (given its computational constraints) always chooses the most moral action. Now, it seems that we could construct an immoral AI system using the following algorithm: Use the moral AI to decide which action of the immoral AI system it would prevent from being taken if it could only choose one action to be prevented. Then take that action. There is a gap in this argument: perhaps the moral AI simply refuses to choose the moral actions in “prevention” decision problems, reasoning that it might currently be used to power an immoral AI. (If exploiting a moral AI was the only way to build other AIs, then this might be the rational thing to do as there might be more exploitation attempts than real prevention scenarios.) Still (without having thought about it too much), it seems likely to me that a more elaborate version of such an argument could succeed.
Here’s a weaker moral realist convergence claim about AI alignment: There’s moral truth and we can program AIs to care about the moral truth. Perhaps it suffices to merely “tell them” to refer to the moral truth when deciding what to do. Or perhaps we would have to equip them with a dedicated “sense” for identifying moral truths. This version of moral realism again does not claim that the orthogonality thesis is wrong, i.e. that sufficiently effective AI systems will automatically behave ethically without us giving them any kind of moral guidance. It merely states that in addition to the straightforward approach of programming an AI to adopt some value system (such as utilitarianism), we could also program the AI to hold the correct moral system. Since pointing at something that exists in the world is often easier than describing that thing, it might be thought that this alternative approach to value loading is easier than the more direct one.
I haven’t found anyone who defends this view (I haven’t looked much), but non-realist Brian Tomasik gives this version of moral realism as a reason to discuss moral realism:
Moral realism is a fun philosophical topic that inevitably generates heated debates. But does it matter for practical purposes? […] One case where moral realism seems problematic is regarding superintelligence. Sometimes it’s argued that advanced artificial intelligence, in light of its superior cognitive faculties, will have a better understanding of moral truth than we do. As a result, if it’s programmed to care about moral truth, the future will go well. If one rejects the idea of moral truth, this quixotic assumption is nonsense and could lead to dangerous outcomes if taken for granted.
(Below, I will argue that there might be no reason to be afraid of moral realists. However, my argument will, like Brian’s, also imply that moral realism is worth debating in the context of AI.)
As an example, consider a moral realist view according to which moral truth is similar to mathematical truth: there are some axioms of morality which are true (for reasons I, as a non-realist, do not understand or agree with) and together these axioms imply some moral theory X. This moral realist view suggests an approach to AI alignment: program the AI to abide by these axioms (in the same way as we can have automated theorem provers assume some set of mathematical axioms to be true). It seems clear that something along these lines could work. However, this approach’s reliance on moral realism is also much weaker.
As a second example, divine command theory states that moral truth is determined by God’s will (again, I don’t see why this should be true and how it could possibly be justified). A divine command theorist might therefore want to program the AI to do whatever God wants it to do.
Here are some more such theories:
- Social contract
- Habermas’ discourse ethics
- Universalizability / Kant’s categorical imperative
- Applying human intuition
Besides pointing being easier than describing, another potential advantage of such a moral realist approach might be that one is more confident in one’s meta-ethical view (“the pointer”) than in one’s object-level moral system (“one’s own description”). For example, someone could be confident that moral truth is determined by God’s will but be unsure that God’s will is expressed via the Bible, the Quran or something else, or how these religious texts are to be understood. Then that person would probably favor AI that cares about God’s will over AI that follows some particular interpretation of, say, the moral rules proposed in the Quran and Sharia.
A somewhat related issue which has received more attention in the moral realism literature is the convergence of human moral views. People have given moral realism as an explanation for why there is near-universal agreement on some ethical views (such as “when religion and tradition do not require otherwise, one shouldn’t torture babies”). Similarly, moral realism has been associated with moral progress in human societies, see, e.g., Huemer (2016). At the same time, people have used the existence of persisting and unresolvable moral disagreements (see, e.g., Bennigson 1996 and Sayre-McCord 2017, sect. 1) and the existence of gravely immoral behavior in some intelligent people (see, e.g., Nichols 2002) as arguments against moral realism. Of course, all of these arguments take moral realism to include a convergence thesis where being a human (and perhaps not being affected by some mental disorders) or a being a society of humans is sufficient to grasp and abide by moral truth.
Of course, there are also versions of moral realism that have even weaker (or just very different) implications for AI alignment and do not make any relevant convergence claims (cf. McGrath 2010). For instance, there may be moral realists who believe that there is a moral truth but that machines are in principle incapable of finding out what it is. Some may also call very different views “moral realism”, e.g. claims that given some moral imperative, it can be decided whether an action does or does not comply with that imperative. (We might call this “hypothetical imperative realism”.) Or “linguistic” versions of moral realism which merely make claims about the meaning of moral statements as intended by whoever utters these moral statements. (Cf. Lukas Gloor’s post on how different versions of moral realism differ drastically in terms of how consequential they are.) Or a kind of “subjectivist realism”, which drops mind-independence (cf. Olson 2014, ch. 2).
Why moral-realism-inspired research on AI alignment might be useful
I can think of many reasons why moral realism-based approaches to AI safety have not been pursued much: AI researchers often do not have a sufficiently high awareness of or interest in philosophical ideas; the AI safety researchers who do – such as researchers at MIRI – tend to reject moral realism, at least the versions with implications for AI alignment; although “moral realism” is popular among philosophers, versions of moral realism with strong implications for AI (à la Peter Singer or David Pearce) might be unpopular even among philosophers (cf. again Lukas’ post on how different versions of moral realism differ drastically in terms of how consequential they are); and so on…
But why am I now proposing to conduct such research, given that I am not a moral realist myself? The main reason (besides some weaker reasons like pluralism and keeping this blog interesting) is that I believe AI alignment research from a moral realist perspective might actually increase agreement between moral realists and anti-realists about how (and to which extent) AI alignment research should be done. In the following, I will briefly argue this case for the strong (à la Peter Singer and David Pearce) and the weak convergence versions of moral realism outlined above.
Strong versions
Like most problems in philosophy, the question of whether moral realism is true lacks an accepted truth condition or an accepted way of verifying an answer or an argument for either realism or anti-realism. This is what makes these problems so puzzling and intractable. This is in contrast to problems in mathematics where it is pretty clear what counts as a proof of a hypothesis. (This is, of course, not to say that mathematics involves no creativity or that there are no general purpose “tools” for philosophy.) However, the claim made by strong convergence moral realism is more like a mathematical claim. Although it is yet to be made precise, we can easily imagine a mathematical (or computer-scientific) hypothesis stating something like this: “For any goal X of some kind [namely the objectively incorrect and non-trivial-to-achieve kind] there is no efficient algorithm that when implemented in a robot achieves X in some class of environments. So, for instance, it is in principle impossible to build a robot that turns Earth into a pile of paperclips.” It may still be hard to formalize such a claim and mathematical claims can still be hard to prove or disprove. But determining the truth of a mathematical statement is not a philosophical problem, anymore. If someone lays out a mathematical proof or disproof of such a claim, any reasonable person’s opinion would be swayed. Hence, I believe that work on proving or disproving this strong version of moral realism will lead to (more) agreement on whether the “strong-moral-realism-based theory of AI alignment” is true.
It is worth noting that finding out whether strong convergence is true may not resolve metaphysical issues. Of course, all strong versions of moral realism would turn out false if the strong convergence hypothesis were falsified. But other versions of moral realism would survive. Conversely, if the strong convergence hypothesis turned out to be true, then anti-realists may remain anti-realists (cf. footnote 2). But if our goal is to make AI moral, the convergence question is much more important than the metaphysical question. (That said, for some people the metaphysical question has a bearing on whether they have preferences over AI systems’ motivation system – “if no moral view is more true than any other, why should I care about what AI systems do?”)
Weak versions
Weak convergence versions of moral realism do not make such in-principle-testable predictions. Their only claim is the metaphysical view that the goals identified by some method X (such as derivation from a set moral axioms, finding out what God wants, discourse, etc.) have some relation to moral truths. Thinking about weak convergence moral realism from the more technical AI alignment perspective is therefore unlikely to resolve disagreements about whether some versions of weak convergence moral realism are true. However, I believe that by not making testable predictions, weak convergence versions of moral realism are also unlikely to lead to disagreement about how to achieve AI alignment.
Imagine moral realists were to propose that AI systems should reason about morality according to some method X on the basis that the result of applying X is the moral truth. Then moral anti-realists could agree with the proposal on the basis that they (mostly) agree with the results of applying method X. Indeed, for any moral theory with realist ambitions, ridding that theory of these ambitions yields a new theory which an anti-realist could defend. As an example, consider Habermas’ discourse ethics and Yudkowsky’s Coherent Extrapolated Volition. The two approaches to justifying moral views seem quite similar – roughly: do what everyone would agree with if they were exposed to more arguments. But Habermas’ theory explicitly claims to be realist while Yudkowsky is a moral anti-realist, as far as I can tell.
In principle, it could be that moral realists defend some moral view on the grounds that it is true even if it seems implausible to others. But here’s a general argument for why this is unlikely to happen. You cannot directly perceive ought statements (David Pearce and others would probably disagree) and it is easy to show that you cannot derive a statement containing an ought without using other statements containing an ought or inference rules that can be used to introduce statements containing an ought. Thus, if moral realism (as I understand it for the purpose of this paper) is true, there must be some moral axioms or inference rules that are true without needing further justification, similar to how some people view the axioms of Peano arithmetic or Euclidean geometry. An example of such a moral rule could be (a formal version of) “pain is bad”. But if these rules are “true without needing further justification”, then they are probably appealing to anti-realists as well. Of course, anti-realists wouldn’t see them as deserving the label of “truth” (or “falsehood”), but assuming that realists and anti-realists have similar moral intuitions, anything that a realist would call “true without needing further justification” should also be appealing to a moral anti-realist.
As I have argued elsewhere, it’s unlikely we will ever come up with (formal) axioms (or methods, etc.) for morality that would be widely accepted by the people of today (or even among today’s Westerners with secular ethics). But I still think it’s worth a try. If it doesn’t work out, weak convergence moral realists might come around to other approaches to AI alignment, e.g. ones based on extrapolating from human intuition.
Other realist positions
Besides realism about morality, there are many other less commonly discussed realist positions, for instance, realism about which prior probability distribution to use, whether to choose according to some expected value maximization principle (and if so which one), etc. The above considerations apply to these other realist positions as well.
Acknowledgment
I wrote this post while working for the Foundational Research Institute, which is now the Center on Long-Term Risk.
1. There are some “universal instrumental goal” approaches to justifying morality. Some are based on cooperation and work roughly like this: “Whatever your intrinsic goals are, it is often better to be nice to others so that they reciprocate. That’s what morality is.” I think such theories fail for two reasons: First, there seem to many widely accepted moral imperatives that cannot be fully justified by cooperation. For example, we usually consider it wrong for dictators to secretly torture and kill people, even if doing so has no negative consequences for them. Second, being nice to others because one hopes that they reciprocate is not, I think, what morality is about. To the contrary, I think morality is about caring things (such as other people’s welfare) intrinsically. I discuss this issue in detail with a focus on so-called “superrational cooperation” in chapter 6.7 of “Multiverse-wide Cooperation via Correlated Decision Making”. Another “universal instrumental goal” approach is the following: If there is at least one god, then not making these gods angry at you may be another universal instrumental goal, so whatever an agent’s intrinsic goal is, it will also act according to what the gods want. The same “this is not what morality is about” argument seems to apply. ↩
2. Yudkowsky has written about why he now rejects this form of moral realism in the first couple of blog posts in the “Value Theory” series. ↩
Goertzel’s GOLEM implements evidential decision theory applied to policy choice
I’ve written about the question of which decision theories describe the behavior of approaches to AI like the “Law of Effect”. In this post, I would like to discuss GOLEM, an architecture for a self-modifying artificial intelligence agent described by Ben Goertzel (2010; 2012). Goertzel calls it a “meta-architecture” because all of the intelligent work of the system is done by sub-programs that the architecture assumes as given, such as a program synthesis module (cf. Kaiser 2007).
Roughly, the top-level self-modification is done as follows. For any proposal for a (partial) self-modification, i.e. a new program to replace (part of) the current one, the “Predictor” module predicts how well that program would achieve the goal of the system. Another part of the system — the “Searcher” — then tries to find programs that the Predictor deems superior to the current program. So, at the top level, GOLEM chooses programs according to some form of expected value calculated by the Predictor. The first interesting decision-theoretical statement about GOLEM is therefore that it chooses policies — or, more precisely, programs — rather than individual actions. Thus, it would probably give the money in at least some versions of counterfactual mugging. This is not too surprising, because it is unclear on what basis one should choose individual actions when the effectiveness of an action depends on the agent’s decisions in other situations.
The next natural question to ask is, of course, what expected value (causal, evidential or other) the Predictor computes. Like the other aspects of GOLEM, the Predictor is subject to modification. Hence, we need to ask according to what criteria it is updated. The criterion is provided by the Tester, a “hard-wired program that estimates the quality of a candidate Predictor” based on “how well a Predictor would have performed in the past” (Goertzel 2010, p. 4). I take this to mean that the Predictor is judged based the extent to which it is able to predict the things that actually happened in the past. For instance, imagine that at some time in the past the GOLEM agent self-modified to a program that one-boxes in Newcomb’s problem. Later, the agent actually faced a Newcomb problem based on a prediction that was made before the agent self-modified into a one-boxer and won a million dollars. Then the Predictor should be able to predict that self-modifying to one-boxing in this case “yielded” getting a million dollar even though it did not do so causally. More generally, to maximize the score from the Tester, the Predictor has to compute regular (evidential) conditional probabilities and expected utilities. Hence, it seems that the EV computed by the Predictor is a regular EDT-ish one. This is not too surprising, either, because as we have seen before, it is much more common for learning algorithms to implement EDT, especially if they implement something which looks like the Law of Effect.
In conclusion, GOLEM learns to choose policy programs based on their EDT-expected value.
Acknowledgements
This post is based on a discussion with Linda Linsefors, Joar Skalse, and James Bell. I wrote this post while working for the Foundational Research Institute, which is now the Center on Long-Term Risk.
Three wagers for multiverse-wide superrationality
In this post, I outline three wagers in favor of the hypothesis that multiverse-wide superrationality (MSR) has action-guiding implications. MSR is based on three core assumptions:
- There is a large or infinite universe or multiverse.
- Applying an acausal decision theory.
- An agent’s actions provide evidence about the actions of other, non-identical agents with different goals in other parts of the universe.
There are three wagers corresponding to these three assumptions. The wagers works only with those value systems that can also benefit from MSR (for instance, with total utilitarianism) (see Oesterheld, 2017, sec. 3.2). I assume such a value system in this post. I am currently working on a longer paper about a wager for (ii), which will discuss the premises for this wager in more detail.
A wager for acausal decision theory and a large universe
If this universe is very large or infinite, then it is likely that there is an identical copy of the part of the universe that is occupied by humans somewhere far-away in space (Tegmark 2003, p. 464). Moreover, there will be vastly many or infinitely many such copies. Hence, for example, if an agent prevents a small amount of suffering on Earth, this will be accompanied by many copies doing the same, resulting in multiple amounts of suffering averted throughout the universe.
Assuming causal decision theory (CDT), the impact of an agent’s copies is not taken into account when making decisions—there is an evidential dependence between the agent’s actions and the actions of their copies, but no causal influence. According to evidential decision theory (EDT), on the other hand, an agent should take such dependences into account when evaluating different choices. For EDT, a choice between two actions on Earth is also a choice between the actions of all copies throughout the universe. The same holds for all other acausal decision theories (i.e., decision theories that take such evidential dependences into account): for instance, for the decision theories developed by MIRI researchers (such as functional decision theory (Yudkowsky and Soares, 2017)), and for Poellinger’s variation of CDT (Poellinger, 2013).
Each of these considerations on its own would not be able to get a wager off the ground. But jointly, they can do so: on the one hand, given a large universe, acausal decision theories will claim a much larger impact with each action than causal decision theory does. Hence, there is a wager in favor of these acausal decision theories. Suppose an agent applies some meta decision theory (see MacAskill, 2016, sec. 2) that aggregates the expected utilities provided by individual decision theories. Even if the agent assigns a small credence to acausal decision theories, these theories will still dominate the meta decision theory’s expected utilities. On the other hand, if an agent applies an acausal decision theory, they can have a much higher impact in a large universe than in a small universe. The agent should thus always act as if the universe is large, even if they only assign a very small credence to this hypothesis.
In conclusion, most of an agent’s impact comes from applying an acausal decision theory in a large universe. Even if the agent assigns a small credence both to acausal decision theories and to the hypothesis that the universe is large, they should still act as if they placed a high credence in both.
A wager in favor of higher correlations
In explaining the third wager, it is important to note that I assume a subjective interpretation of probability. If I say that there is a correlation between the actions of two agents, I mean that, given one’s subjective beliefs, observing one agent’s action provides evidence about the other agent’s action. Moreover, I assume that agents are in a symmetrical decision situation—for instance, this is the case for two agents in a prisoner’s dilemma. If the decision situation is symmetrical, and if the agents are sufficiently similar, their actions will correlate. The theory of MSR says that agents in a large universe probably are in a symmetrical decision situation (Oesterheld, 2017, sec. 2.8).
There exists no general theory of correlations between different agents. It seems plausible to assume that a correlation between the actions of two agents must be based on a logical correlation between the decision algorithms that these two agents implement. But it is not clear how to think about the decision algorithms that humans implement, for instance, and how to decide whether two decision algorithms are functionally equivalent (Yudkowsky and Soares, sec. 3). There exist solutions to these problems only in some narrow domains—for instance, for agents represented by programs written in some specific programming language.
Hence, it is also not clear which agents’ actions in a large universe correlate, given that all are in a symmetrical decision situation. It could be that an agent’s actions correlate only with very close copies. If these copies thus share the same values as the agent, then MSR does not have any action-guiding consequences. The agent will just continue to pursue their original goal function. If, on the other hand, there are many correlating agents with different goals, then MSR has strong implications. In the latter case, there can be gains from trade between these agents’ different value systems.
Just as there is a wager for applying acausal decision theory in general, there is also a wager in favor of assuming that an agent’s actions correlate with more rather than fewer different agents. Suppose there are two hypotheses: (H1) Alice’s actions only correlate with the actions of (G1) completely identical copies of Alice, and (H2) Alice’s actions correlate with (G2) all other agents that ever gave serious consideration to MSR or some equivalent idea.
(In both cases, I assume that Alice has seriously considered MSR herself.) G1 is a subset of G2, and it is plausible that G2 is much larger than G1. Moreover, it is plausible that there are also agents with Alice’s values among the agents in G2 which are not also in G1. Suppose 1-p is Alice’s credence in H1, and p her credence in H2. Suppose further that there are n agents in G1 and m agents in G2, and that q is the fraction of agents in G2 sharing Alice’s values. All agents have the choice between (A1) only pursuing their own values, and (A2) pursuing the sum over the values of all agents in G2. Choosing A1 gives an agent 1 utilon. Suppose g denotes the possible gains from trade; that is, choosing A2 produces (1+g)×s utilons for each value system, where s is the fraction of agents in G2 supporting that value system. If everyone in G2 chooses A2, this produces (1+g)×q×m utilons for Alice’s value system, while, if everyone chooses A1, this produces only q×m utilons in total for Alice.
The decision situation for Alice can be summarized by the following choice matrix (assuming, for simplicity, that all correlations are perfect):
| H1 | H2 | |
|---|---|---|
| A1 | n+c | q×m |
| A2 | (1+g)×q×n+c | (1+g)×q×m |
Here, the cells denote the expected utilities that EDT assigns to either of Alice’s actions given either H1 or H2. c is a constant that denotes the expected value generated by the agents in G2 that are non-identical to Alice, given H1. It plays no role in comparing A1 and A2, since, given H1, these agents are not correlated with Alice: the value will be generated no matter which action she picks. The value for H1∧A2 is unrealistically high, since it supposes the same gains from trade as H2∧A2, but this does not matter here. According to EDT, Alice should choose A2 over A1 iff
g×p×q×m > (1-p)×n – (1+g)×(1-p)×n×q.
It seems likely that q×m is larger than n—the requirement that an agent must be a copy of Alice restricts the space of agents more than that of having thought about MSR and sharing Alice’s values. Therefore, even if the gains from trade and Alice’s credence in H2 (i.e., g×p) are relatively small, g×p×q×m is still larger than n, and EDT recommends A2.
While the argument for this wager is not as strong as the argument for the first two wagers, it is still plausible. It is plausible that there are much more agents having thought about MSR and sharing a person’s values than there are identical copies of the person. Hence, if the person’s actions correlate with the actions of all the agents in the larger group, the person’s actions have a much higher impact. Moreover, in this case, they plausibly also correlate with the actions of many agents holding different values, allowing for gains from trade. Therefore, one should act as if there were more rather than fewer correlations, even if one assigns a rather low credence to that hypothesis.
Acknowledgements
I am grateful to Caspar Oesterheld and Max Daniel for helpful comments on a draft of this post. I wrote this post while working for the Foundational Research Institute, which is now the Center on Long-Term Risk.
A wager against Solomonoff induction
The universal prior assigns zero probability to non-computable universes—for instance, universes that could only be represented by Turing machines in which uncountably many locations need to be updated, or universes in which the halting problem is solved in physics. While such universes might very likely not exist, one cannot justify assigning literally zero credence to their existence. I argue that it is of overwhelming importance to make a potential AGI assign a non-zero credence to incomputable universes—in particular, universes with uncountably many “value locations”.
Here, I assume a model of universes as sets of value locations. Given a specific goal function, each element in such a set could specify an area in the universe with some finite value. If a structure contains a sub-structure, and both the structure and the sub-structure are valuable in their own regard, there could either be one or two elements representing this structure in the universe’s set of value locations. If a structure is made up of infinitely many sub-structures, all of which the goal function assigns some positive but finite value to, then this structure could (if the sum of values does not converge) possibly only be represented by infinitely many elements in the set. If the set of value locations representing a universe is countable, then the value of said universe could be the sum over the values of all elements in the set (granted that some ordering of the elements is specified). I write that a universe is “countable” if it can be represented by a finite or countably infinite set, and a universe is “uncountable” if it can only be represented by an uncountably infinite set.
A countable universe, for example, could be a regular cellular automaton. If the automaton has infinitely many cells, then, given a goal function such as total utilitarianism, the automaton could be represented by a countably infinite set of value locations. An uncountable universe, on the other hand, could be a cellular automaton in which there is a cell for each real number, and interactions between cells over time are specified by a mathematical function. Given some utility functions over such a universe, one might be able to represent the universe only by an uncountably infinite set of value locations. Importantly, even though the universe could be described in logic, it would be incomputable.
Depending on one’s approach to infinite ethics, an uncountable universe could matter much more than a countable universe. Agents in uncountable universes might—with comparatively small resource investments—be able to create (or prevent), for instance, amounts of happiness or suffering that could not be created in an entire countable universe. For instance, each cell in the abovementioned cellular automaton might consist of some (possibly valuable) structure in of itself, and the cells’ structures might influence each other. Moreover, some (uncountable) set of cells might be regarded as an agent. The agent might then be able to create a positive amount of happiness in uncountably many cells, which—at least given some definitions of value and approaches to infinite ethics—would have created more value than could ever be created in a countable universe.
Therefore, there is a wager in favor of the hypothesis that humans actually live in an uncountable universe, even if it appears unlikely given current scientific evidence. But there is also a different wager, which applies if there is a chance that such a universe exists, regardless of whether humans live in that universe. It is unclear which of the two wagers dominates.
The second wager is based on acausal trade: there might be agents in an uncountable universe that do not benefit from the greater possibilities of their universe—e.g., because they do not care about the number of individual copies of some structure, but instead care about an integral over the structures’ values relative to some measure over structures. While agents in a countable universe might be able to benefit those agents equally well, they might be much worse at satisfying the values of agents with goals sensitive to the greater possibilities in uncountable universes. Thus, due to different comparative advantages, there could be great gains from trade between agents in countable and uncountable universes.
The above example might sound outlandish, and it might be flawed in that one could not actually come up with interaction rules that would lead to anything interesting happening in the cellular automaton. But this is irrelevant. It suffices that there is only the faintest possibility that an AGI could have an acausal impact in an incomputable universe which, according to one’s goal function, would outweigh all impact in all computable universes. There probably exists a possible universe like that for most goal functions. Therefore, one could be missing out on virtually all impact if the AGI employs Solomonoff induction.
There might not only be incomputable universes represented by a set that has the cardinality of the continuum, but there might be incomputable universes represented by sets of any cardinality. In the same way that there is a wager for the former, there is an even stronger wager for universes with even higher cardinalities. If there is a universe of highest cardinality, it appears to make sense to optimize only for acausal trade with that universe. Of course, there could be infinitely many different cardinalities, so one might hope that there is some convergence as to the values of the agents in universes of ever higher cardinalities (which might make it easier to trade with these agents).
In conclusion, there is a wager in favor of considering the possibility of incomputable universes: even a small acausal impact (relative to the total resources available) in an incomputable universe could counterbalance everything humans could do in a computable universe. Crucially, an AGI employing Solomonoff induction will not consider this possibility, hence potentially missing out on unimaginable amounts of value.
Acknowledgements
Caspar Oesterheld and I came up with the idea for this post in a conversation. I am grateful to Caspar Oesterheld and Max Daniel for helpful feedback on earlier drafts of this post.